파이겐바움 상수
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
파이겐바움 상수는 주기 배가 분기를 보이는 동역학계에서 나타나는 두 개의 상수, 제1 파이겐바움 상수(δ)와 제2 파이겐바움 상수(α)를 의미한다. 제1 상수는 분기 간격의 극한 비율을 나타내며, 제2 상수는 날의 너비 비율을 나타낸다. 이 상수들은 로지스틱 맵과 같은 비선형 맵과 만델브로 집합과 같은 프랙탈 구조에서 관찰되며, 보편성을 지녀 다양한 시스템의 거동 예측에 활용된다. 두 상수는 초월수로 여겨지나 아직 증명되지 않았으며, 보편성에 대한 최초의 증명은 컴퓨터를 이용하여 이루어졌다.
더 읽어볼만한 페이지
- 분기 이론 - 분기 다이어그램
분기 다이어그램은 동역학계에서 분기 매개변수의 변화에 따라 시스템의 고정점, 주기 궤도, 카오스적 끌개가 어떻게 변하는지 보여주는 도표로, 시스템의 안정성을 분석하고 예측하는 데 응용된다. - 분기 이론 - 분기 (동역학계)
분기는 동역학계에서 매개변수 변화에 따라 평형점, 주기 궤도 등의 질적 변화가 발생하는 현상이며, 국소적 분기와 대역적 분기로 나뉜다. - 혼돈 이론 - 창발
창발은 부분에는 없던 성질이 전체에서 나타나는 현상으로, 철학적으로는 요소의 속성으로 설명할 수 없는 체계의 특징을 의미하며, 복잡계 과학, 생명 현상 등 다양한 분야에서 중요한 개념으로 다뤄진다. - 혼돈 이론 - 난류 (역학)
난류는 유체의 불규칙하고 무작위적인 운동 상태로, 일상생활과 공학 등 다양한 분야에서 관찰되며 여러 특징을 설명하기 위한 연구가 진행 중이다. - 수학 상수 - 허수 단위
허수 단위 i는 i² = −1을 만족하는 수로, 실수 체계에서는 정의되지 않는 음수의 제곱근을 나타내며 복소수 체계의 기본 구성 요소로서 복소평면에서 90° 회전하는 효과를 가지며 1, i, -1, -i를 주기적으로 순환하는 특징을 가진다. - 수학 상수 - 실베스터 수열
실베스터 수열은 각 항이 이전 항들의 곱에 1을 더한 값으로 정의되는 정수 수열로서, 재귀적으로 정의되며 이중 지수 함수적으로 증가하고, 이집트 분수 및 탐욕 알고리즘과 관련이 있으며, 역수 합은 1로 수렴한다.
2. 역사
파이겐바움은 처음에는 첫 번째 상수를 주기 배가 분기에서의 로지스틱 맵과 관련시켰지만, 단일 이차 함수 극대와 극소를 가진 모든 1차원 맵에서도 성립한다는 것을 보여주었다.[2][3] 이러한 일반성의 결과로, 이 설명에 해당하는 모든 카오스 시스템은 동일한 속도로 분기할 것이다. 파이겐바움은 1975년에 이 발견을 했고,[2][3] 1978년에 공식적으로 발표했다.[4]
파이겐바움 상수는 주기 배가 분기에서 나타나는 두 가지 수학 상수이다. 제1 파이겐바움 상수(δ)는 분기 간격의 비율과 관련된 상수이고, 제2 파이겐바움 상수(α)는 분기 폭의 비율과 관련된 상수이다.
3. 정의
:
:
이 상수들은 물이 떨어지는 수도꼭지에서 인구 증가에 이르기까지 광범위한 종류의 역학계에서 나타난다.[9]
다음과 같은 차분 방정식에서,
:
값의 변화에 따라 분기가 발생할 때, 파이겐바움 상수들은 다음과 같이 정의된다.[19]
:
:
여기서 는 번째 주기 배가 분기점에서의 값, 는 주기 진동에서 0에 가까운 쪽 분기 폭이다.
3. 1. 제1 파이겐바움 상수 (δ)
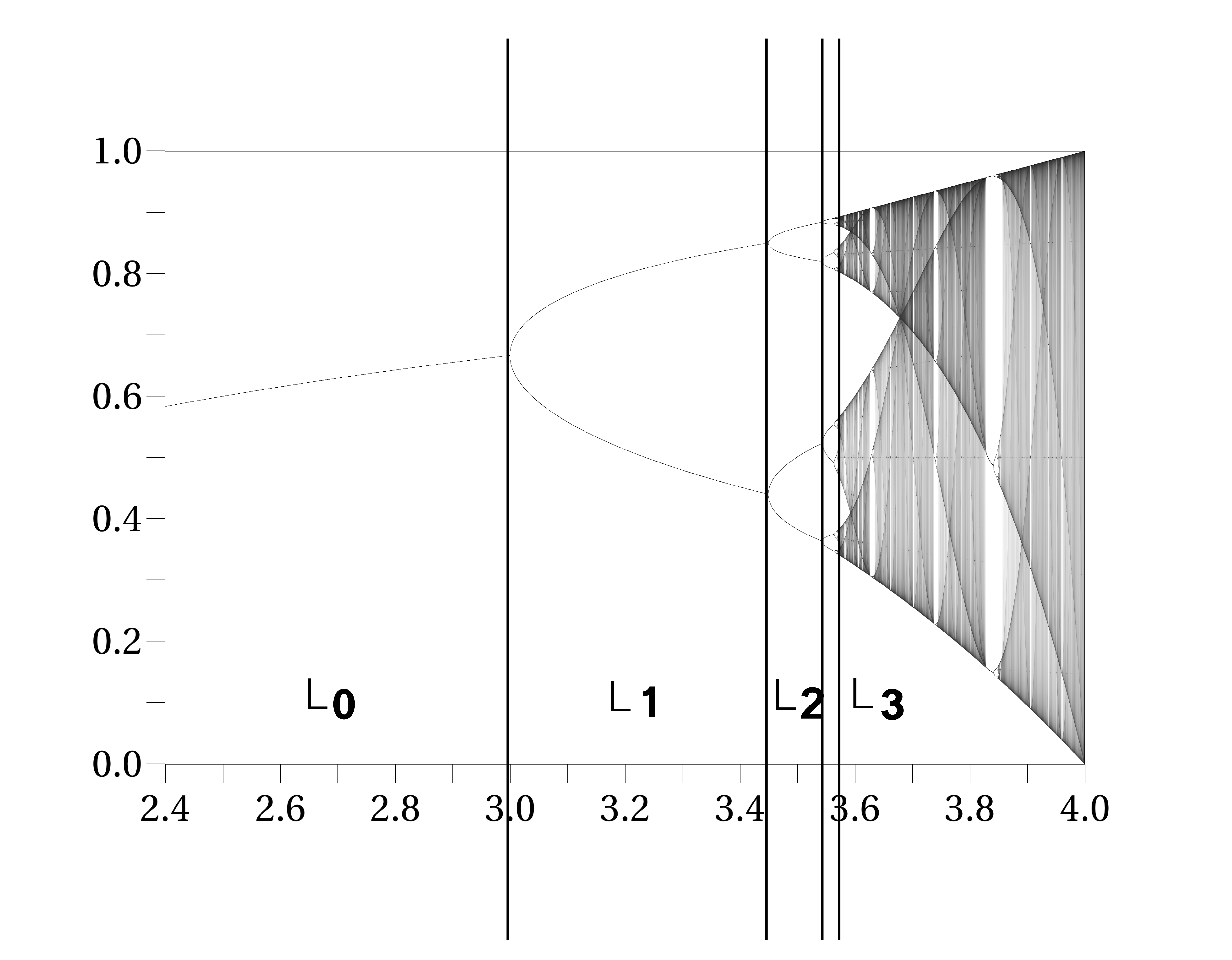
제1 파이겐바움 상수(δ)는 한 모수 맵의 각 주기 배가 분기 사이의 각 분기 간격의 극한 비율이다. 이는 다음과 같은 차분 방정식에서 정의된다.
:
여기서 f(x)는 분기 모수 a로 매개변수화된 함수이다.
δ는 다음과 같은 극한으로 주어진다.
:
여기서 an은 n번째 주기 배가에서 a의 이산 값이다.
이 값은 다음과 같다.
:
한국에서는 이 값을 소수점 이하 여섯 자리까지 반올림하여 4.669202로 사용하는 경우가 많다.
파이겐바움 상수 δ는 분기 구간 L에 대한 연속적인 분기 다이어그램 사이의 거리 비의 한계를 나타낸다. 아래 표는 분기 다이어그램으로부터 얻어지는 파이겐바움 상수의 대략적인 과정을 보여준다. (첫 번째 분기점을 수렴값이 처음으로 0에서 벗어나는 a=1으로 하면 L0 = 2이다.)
다음과 같은 차분 방정식의 μ 변화에 따른 분기에서,
:
첫 번째 파이겐바움 상수 δ는,
:
로 주어진다[19]。위의 차분 방정식에서는 주기 배가 분기가 발생하며, i번째 주기 배가 분기마다 xn의 거동은 2i 주기 진동으로 변화한다[19]。 여기서, μi는 i번째 주기 배가 분기점에서의 μ의 값이다.
3. 2. 제2 파이겐바움 상수 (α)
'''두 번째 파이겐바움 상수''' 또는 '''파이겐바움 축소 매개변수'''[5] α는 다음과 같다.:2.502907875095892822283902873218...
이 값은 날의 너비와 두 개의 하위 날 중 하나의 너비 간의 비율이다(접힘에 가장 가까운 날 제외). 하위 날과 날의 너비 간의 비율을 측정할 때에는 α에 음수 부호가 적용된다.[9]
이 상수들은 광범위한 종류의 역학계에 적용된다(예: 물이 떨어지는 수도꼭지에서 인구 증가까지).[9]
간단한 유리수 근사는 13/11 × 17/11 × 37/27 = 8177/3267이다.
다음과 같은 차분 방정식의 μ 변화에 따른 분기에서,
:xn+1=f(xn)= 1-μ |xn|z, (z>0, n=1, 2, 3, ⋯)
첫 번째 파이겐바움 상수 δ는,
:δz = limi→∞ (μi - μi-1)/(μi+1 - μi)
두 번째 파이겐바움 상수 α는,
:αz = limi→∞ di/di+1
로 주어진다.[19]
위의 차분 방정식에서는 주기 배가 분기가 발생하며, i번째 주기 배가 분기마다 xn의 거동은 2i 주기 진동으로 변화한다.[19] 여기서, μi는 i번째 주기 배가 분기점에서의 μ의 값, di는 2i 주기 진동에서의 0에 가까운 쪽 분기의 폭이다.
z의 값에 따라, δz, αz의 값은 변화한다.[19]
4. 분기 다이어그램과의 관계
파이겐바움 상수는 분기 다이어그램에서 연속적인 분기 간격 사이의 거리 비의 극한값으로 나타난다.[1]
분기 다이어그램에서 분기 간격 의 비 는 이 무한대로 갈수록 파이겐바움 상수 에 수렴한다.
:
4. 1. 분기 다이어그램의 구간
파이겐바움 상수는 분기 다이어그램에서 연속적인 분기 구간 사이의 거리 비의 극한값으로 나타난다. 여기서 분기 구간을 이라 하면, 다음과 같다.
:
아래는 위 분기 다이어그램으로부터 얻어지는 파이겐바움 상수를 구하는 과정이다. (첫 번째 분기점을 수렴값이 처음으로 0에서 벗어나는 으로 하면 이다.)
5. 비선형 맵의 예
파이겐바움 상수를 나타내는 비선형 맵으로는 , , 프랙탈 등이 있다.
에서 a는 분기 매개변수, x는 변수이다. 주기가 두 배가 되는 a의 값은 아래 표와 같이 나타난다.[7]
마지막 열의 비율은 첫 번째 파이겐바움 상수로 수렴한다. 로지스틱 맵 에서도 동일한 숫자가 나타난다.[8]
5. 1. 로지스틱 맵

로지스틱 맵은 파이겐바움 상수를 보여주는 대표적인 예시이다. 여기서 a는 분기 매개변수, x는 변수이다.
이 숫자가 어떻게 나타나는지 보기 위해, 다음과 같은 1개의 매개변수를 갖는 로지스틱 맵을 생각해 보자.
:
주기가 두 배가 되는 a의 값(예: 주기-2 궤도가 없는 가장 큰 a 값, 또는 주기-4 궤도가 없는 가장 큰 a 값)은 a1, a2 등이다. 이들은 아래 표에 정리되어 있다.[8]
마지막 열의 비율은 첫 번째 파이겐바움 상수로 수렴한다.
5. 2. 다른 비선형 맵
로지스틱 맵 외에도 파이겐바움 상수를 관찰할 수 있는 비선형 맵에는 다음과 같은 것들이 있다.다음은 의 로지스틱 맵을 processing.js를 사용하여 표현한 것이다.
이 숫자가 어떻게 나타나는지 보기 위해, 1개의 매개변수를 갖는 실수 맵 를 생각해 보자. 여기서 a는 분기 매개변수이고, x는 변수이다. 주기가 두 배가 되는 a의 값(예: 주기-2 궤도가 없는 가장 큰 a 값, 또는 주기-4 궤도가 없는 가장 큰 a 값)은 a1, a2 등이다. 이들은 아래 표에 정리되어 있다.[7]
마지막 열의 비율은 첫 번째 파이겐바움 상수로 수렴한다. 동일한 숫자는 실수 매개변수 a와 변수 x를 갖는 로지스틱 맵 에도 나타난다. 다음은 분기 값을 표로 정리한 것이다.[8]
6. 프랙탈과의 관계
파이겐바움 상수는 프랙탈 구조에서도 나타난다.
복소 이차 다항식
:
의 만델브로 집합에서 파이겐바움 상수는 복소 평면에서 실수선상의 연속적인 원들의 지름 사이의 극한 비율이다. 분기 매개변수는 주기 구성 요소의 근 지점인데, 이 계열은 '''파이겐바움 점''' = −1.401155......로 수렴한다.
분기 이론에서 파이겐바움 상수는 기하학의 π 및 미적분학의 e와 유사하게 다른 맵에서도 이 비율을 재현한다.
6. 1. 만델브로 집합
복소 이차 다항식
:
의 만델브로 집합의 경우, 파이겐바움 상수는 복소 평면에서 실수선상의 연속적인 원들의 지름 사이의 극한 비율이다(오른쪽의 애니메이션 참조).
분기 매개변수는 주기 구성 요소의 근 지점이다. 이 계열은 '''파이겐바움 점''' = −1.401155......로 수렴한다. 마지막 열의 비율은 첫 번째 파이겐바움 상수로 수렴한다.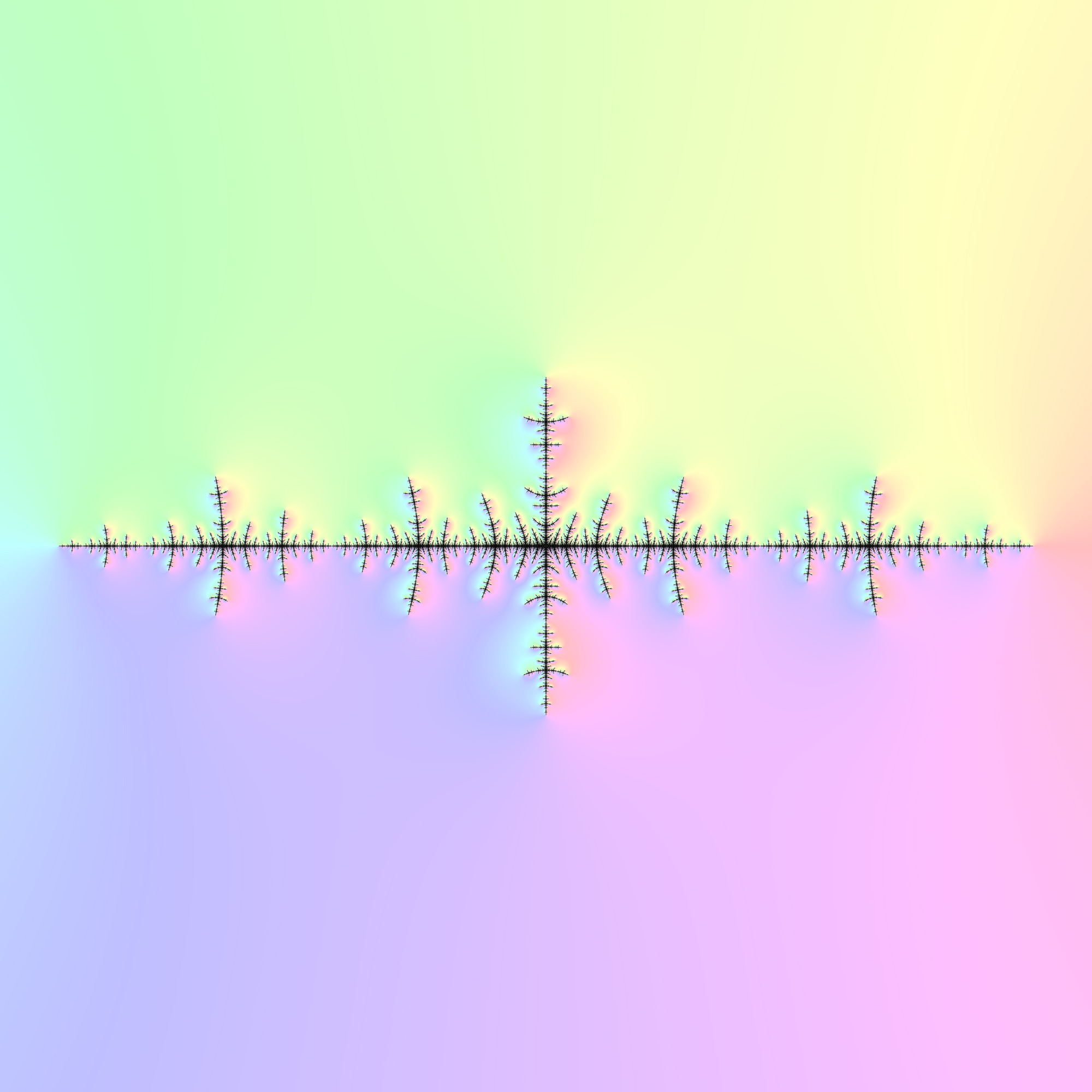
다른 맵들도 이 비율을 재현한다. 이런 의미에서 분기 이론에서 파이겐바움 상수는 기하학의 π 및 미적분학의 e와 유사하다.
6. 2. 줄리아 집합
줄리아 집합은 만델브로 집합과 관련된 또 다른 프랙탈 구조이다. 파이겐바움 점에서의 줄리아 집합은 파이겐바움 상수를 시각적으로 보여준다.
7. 성질
두 상수 모두 초월수로 여겨지지만, 아직 수학적 증명되지는 않았다.[10] 실제로, 두 상수 중 어느 것이라도 무리수라는 증명조차 알려진 바가 없다.
8. 다른 값
로지스틱 맵의 주기 3 창 역시 혼돈으로 가는 주기 배증 경로를 가지며, 에서 혼돈에 도달하고, 자체적인 두 개의 파이겐바움 상수 을 갖는다.[4]
참조
[1]
Youtube
The Feigenbaum Constant (4.669) – Numberphile
https://www.youtube.[...]
2017-01-16
[2]
논문
Universality in complex discrete dynamics
http://chaosbook.org[...]
[3]
서적
Chaos: An Introduction to Dynamical Systems
Springer
[4]
논문
Quantitative universality for a class of nonlinear transformations
1978
[5]
웹사이트
Feigenbaum Constant
https://mathworld.wo[...]
2024-10-06
[6]
서적
Non-Linear Ordinary Differential Equations: Introduction for Scientists and Engineers
Oxford University Press
[7]
서적
Alligood
https://books.google[...]
[8]
서적
Alligood
https://books.google[...]
[9]
서적
Nonlinear Dynamics and Chaos
Perseus Books
[10]
학위논문
Feigenbaum scaling in discrete dynamical systems
http://keithbriggs.i[...]
University of Melbourne
[11]
논문
A computer-assisted proof of the Feigenbaum conjectures
[12]
논문
A complete proof of the Feigenbaum conjectures
[13]
논문
Feigenbaum-Coullet-Tresser universality and Milnor's Hairiness Conjecture
[14]
논문
Dependence of universal constants upon multiplication period in nonlinear maps
https://link.aps.org[...]
1985-01-01
[15]
서적
Chaos and nonlinear dynamics: an introduction for scientists and engineers
Oxford University Press
2000
[16]
웹사이트
Calculation of the Feigenbaum Constants
http://www.harald-ho[...]
2015-10-25
[17]
웹사이트
Feigenbaum Constant
http://mathworld.wol[...]
Wolfram Research
2014-09-20
[18]
학위논문
Feigenbaum scaling in discrete dynamical systems
http://keithbriggs.i[...]
University of Melbourne
[19]
논문
A Precise Calculation of the Feigenbaum Constants
http://www.ams.org/j[...]
American Mathematical Society
1991-07
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
![파이겐바움 상수 {{mvar|δ}}는 {{math|''L<sub>i</sub>'' /''L''<sub>''i'' + 1</sub>}}에서 연속적인 분기 다이어그램 사이의 거리의 [[극한 (수학)|극한]]을 나타낸다.](https://cdn.onul.works/wiki/noimage.png)